
늦깎이연구소 | 바둑 AI 개발기 #3
체스와 바둑의 결정적 차이
체스 AI는 1990년대에 이미 세계 챔피언을 이겼다.
하지만 바둑 AI는 2016년이 되어서야 성공했다.
왜 20년이나 차이가 날까?
분기 계수(Branching Factor) 때문이다.
체스: 평균 35개의 선택지 바둑: 평균 250개의 선택지 (19x19 기준)
체스에서 쓰던 방법 — 미니맥스(Minimax) — 은
모든 가능한 수를 탐색한다.
하지만 바둑에서는?
차원의 저주(Curse of Dimensionality).
가능한 경우의 수가 우주의 원자 수보다 많다.
발상의 전환: 전부 보지 말자
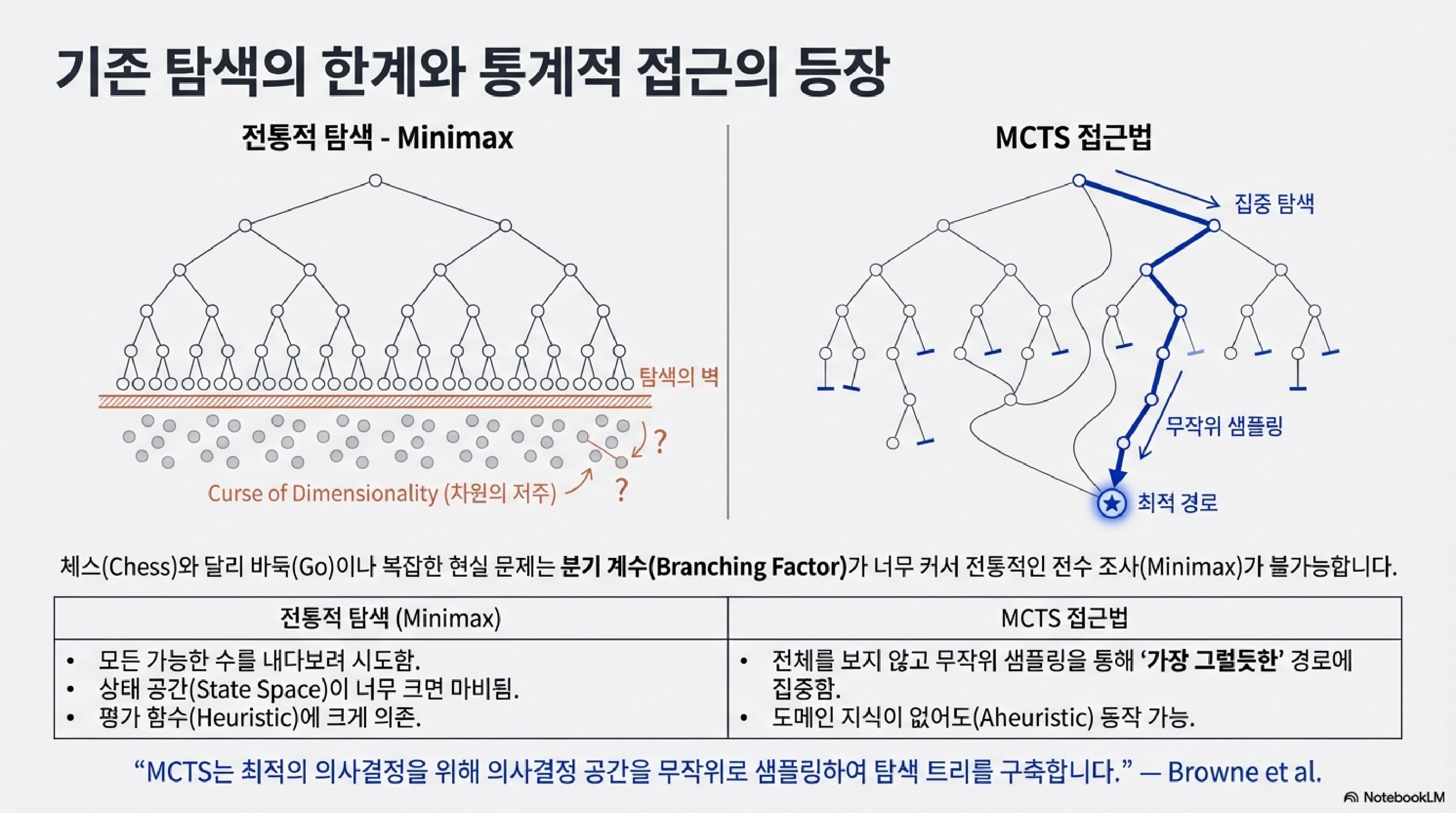
전통적 탐색 (Minimax):
- 모든 가능한 수를 내다보려 시도함
- 상태 공간(State Space)이 너무 크면 마비됨
- 평가 함수(Heuristic)에 크게 의존
MCTS의 접근법:
- 전체를 보지 않고 무작위 샘플링
- 가장 그럴듯한 경로에 집중
- 도메인 지식이 없어도(Aheuristic) 동작 가능
“MCTS는 최적의 의사결정을 위해 의사결정 공간을 무작위로 샘플링하여 탐색 트리를 구축합니다.”
— Browne et al.
MCTS의 4단계 순환
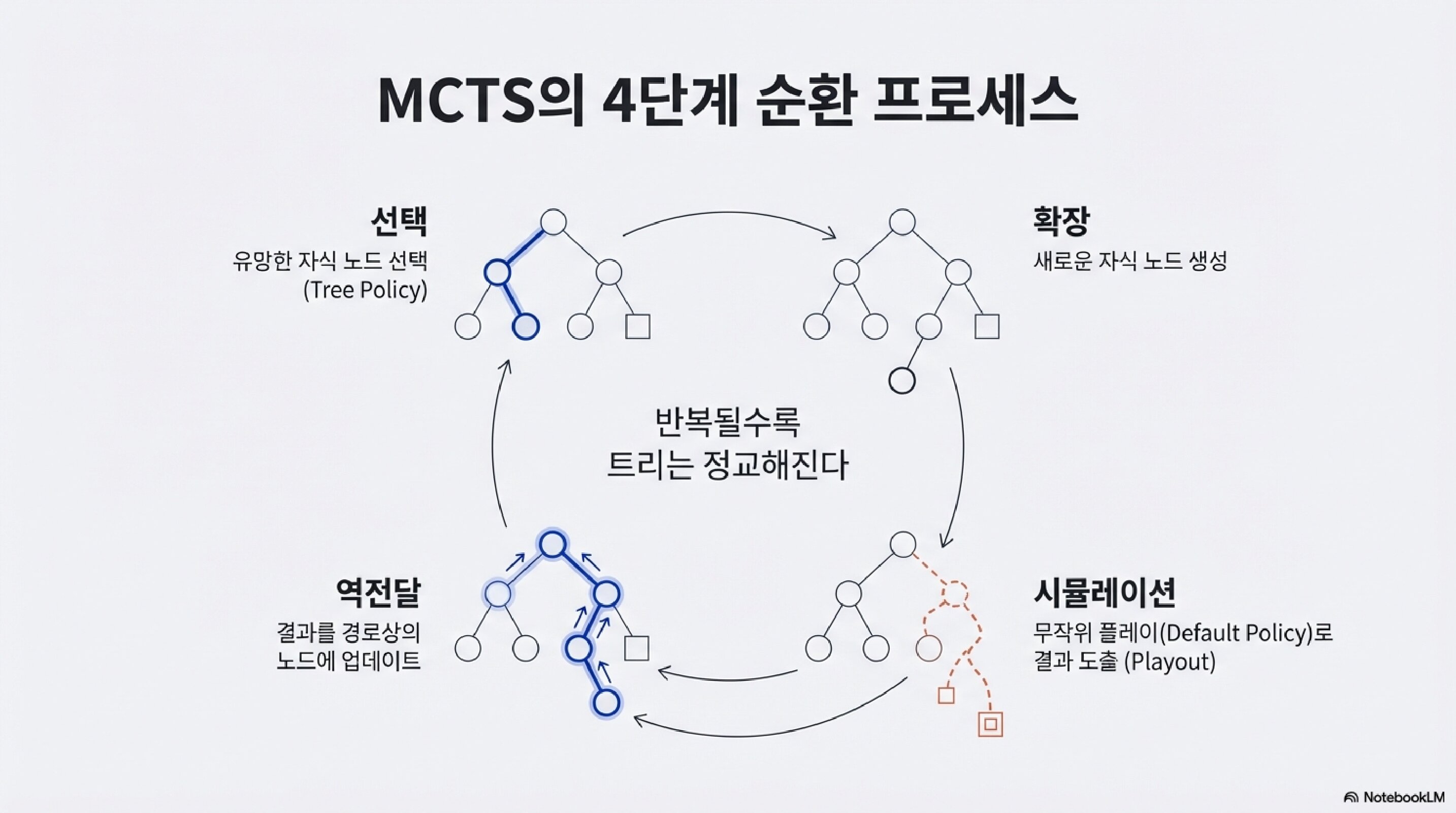
MCTS는 4단계를 무한히 반복한다.
반복할수록 트리는 정교해진다.
1단계: 선택 (Selection)
현재 트리에서 가장 유망해 보이는 경로를 따라 내려간다.
“유망하다”의 기준은 곧 설명할 UCT 공식이 결정한다.
2단계: 확장 (Expansion)
아직 탐색하지 않은 새로운 수를 트리에 추가한다.
3단계: 시뮬레이션 (Simulation)
새 노드에서 게임이 끝날 때까지 무작위로 둔다.
이걸 플레이아웃(Playout) 또는 롤아웃(Rollout) 이라고 한다.
4단계: 역전파 (Backpropagation)
시뮬레이션 결과(승/패)를 거쳐온 모든 노드에 기록한다.
비대칭적 트리의 성장
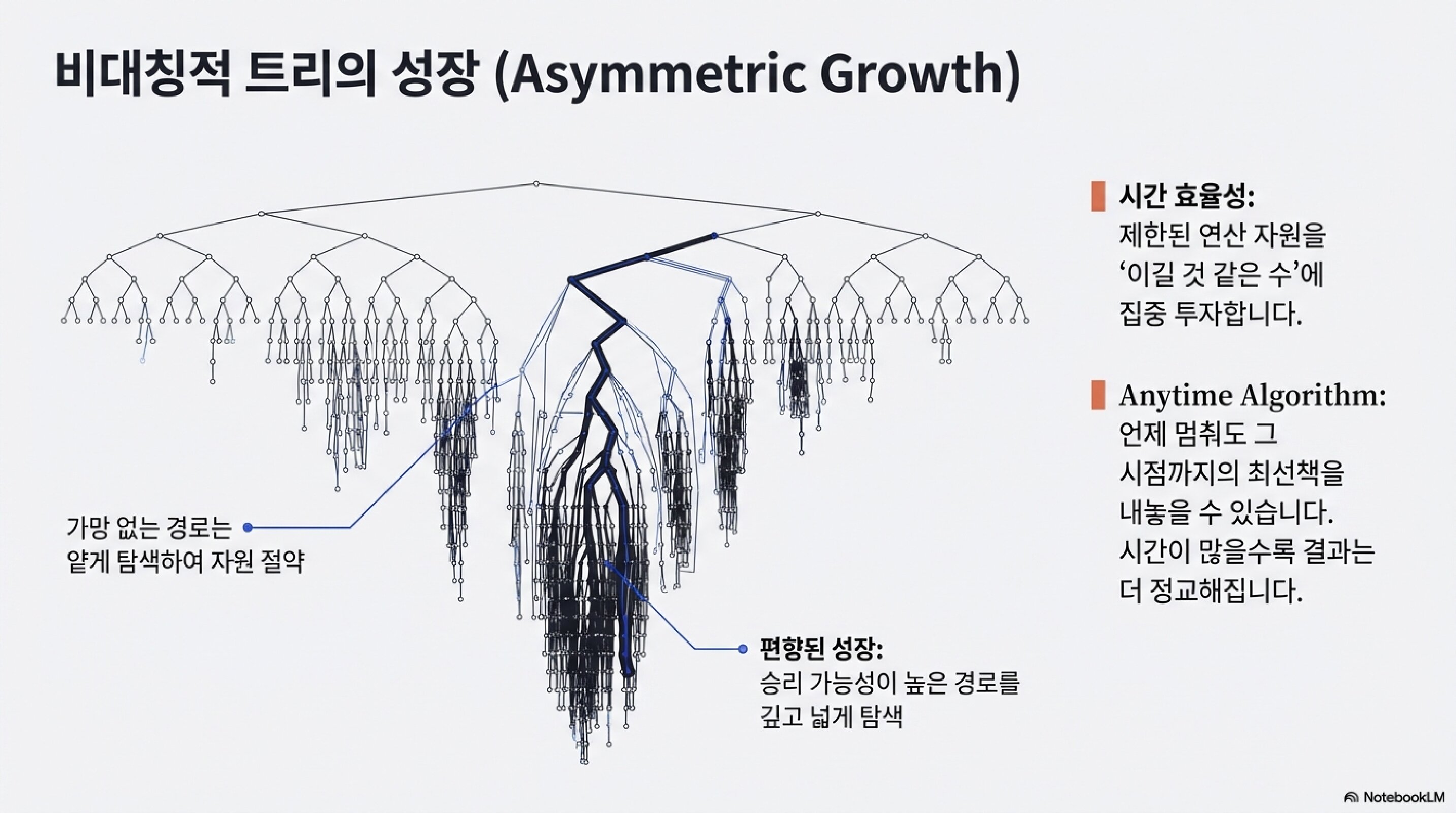
MCTS의 핵심 특성이 여기 있다.
모든 가지를 균등하게 탐색하지 않는다.
유망한 경로에 집중 투자한다.
시간 효율성
제한된 연산 자원을 이길 것 같은 수에 집중 투자한다.
Anytime Algorithm
언제 멈춰도 그 시점까지의 최선책을 내놓을 수 있다.
시간이 많을수록 결과는 더 정교해진다.
탐험과 활용의 딜레마
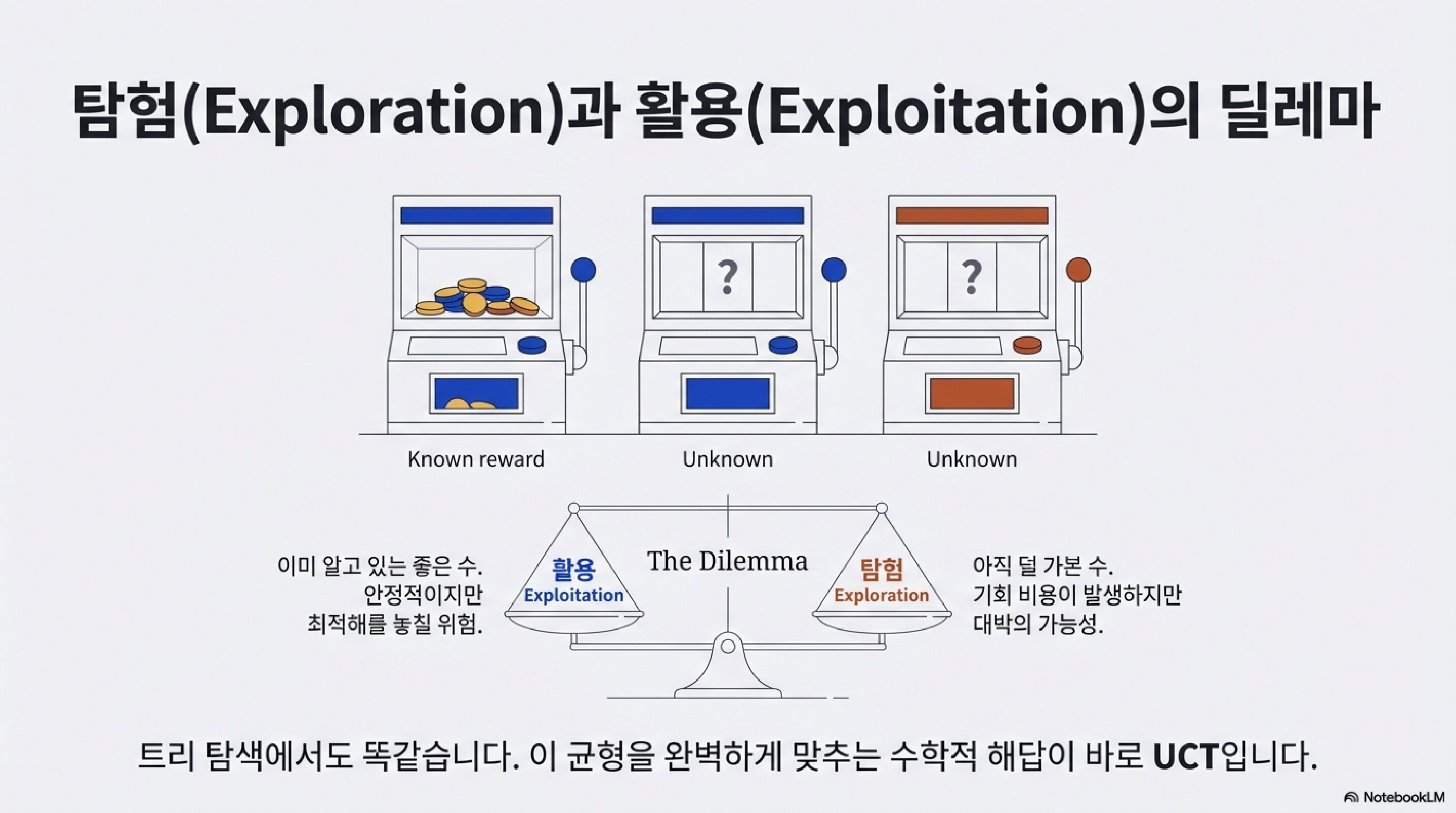
여기서 근본적인 질문이 생긴다.
슬롯머신 3대가 있다고 상상해보자.
기계 1은 어느 정도 보상을 주는지 알고 있다.
기계 2, 3은 아직 모른다.
활용(Exploitation): 이미 알고 있는 좋은 수.
안정적이지만 최적해를 놓칠 위험.
탐험(Exploration): 아직 덜 가본 수.
기회 비용이 발생하지만 대박의 가능성.
트리 탐색에서도 똑같다.
이 균형을 완벽하게 맞추는 수학적 해답이 바로 UCT다.
UCT 알고리즘: 불확실성을 제어하는 수식

활용 항: w_i / n_i
- 승수 / 방문 횟수
- 현재 승률이 높을수록 선택
탐험 항: c × √(ln(N)/n_i)
- 방문 횟수가 적을수록 값이 커짐
- 덜 가본 길을 선택하게 유도 (호기심 항)
c는 탐험 상수.
이 값을 조절해서 탐험과 활용의 균형을 맞춘다.
Kocsis와 Szepesvári(2006) 증명:
이 수식을 사용하면 무한한 시간 내에 이론적으로 최적해(Minimax)에 수렴한다.
MCTS의 다양한 변형
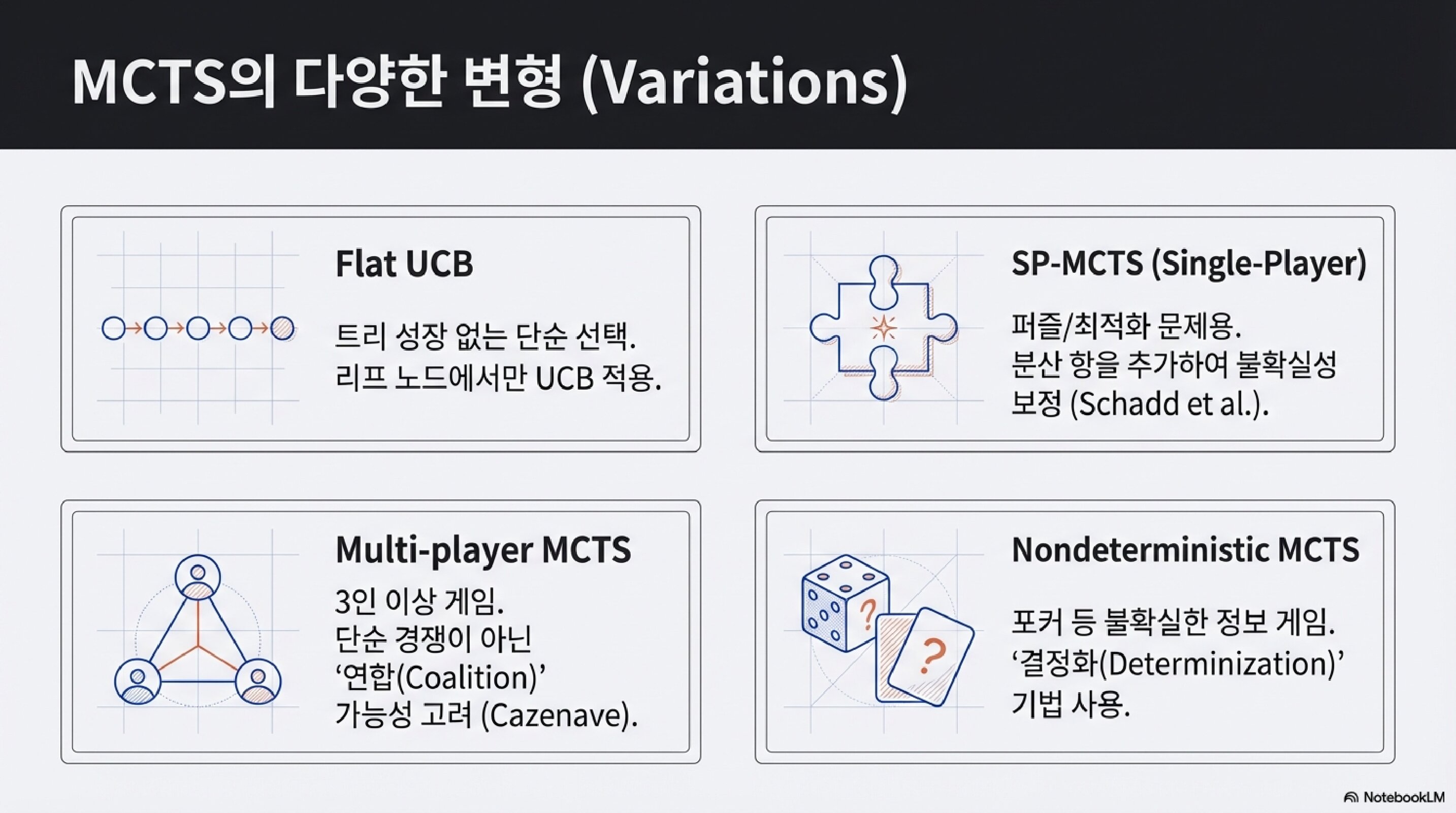
MCTS는 하나의 알고리즘이 아니라 프레임워크다.
다양한 변형이 존재한다.
Flat UCB
트리 성장 없는 단순 선택. 리프 노드에서만 UCB 적용.
SP-MCTS (Single-Player)
퍼즐/최적화 문제용. 분산 항을 추가하여 불확실성 보정.
Multi-player MCTS
3인 이상 게임. 단순 경쟁이 아닌 연합(Coalition) 가능성 고려.
Nondeterministic MCTS
포커 등 불확실한 정보 게임. 결정화(Determinization) 기법 사용.
성능 향상 기법 1: 더 똑똑하게 선택하기
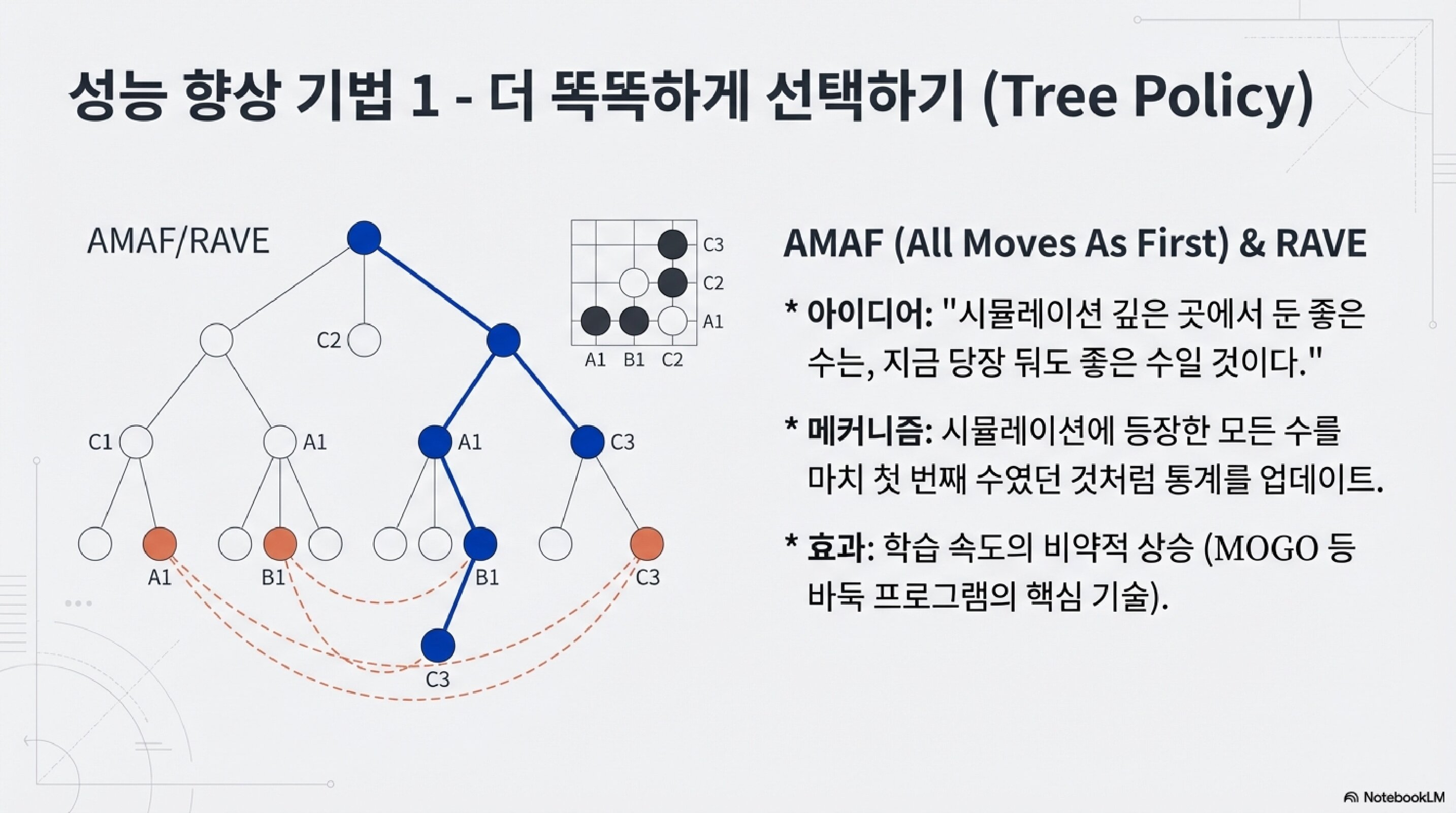
AMAF (All Moves As First) & RAVE
아이디어: “시뮬레이션 깊은 곳에서 둔 좋은 수는, 지금 당장 둬도 좋은 수일 것이다.”
메커니즘: 시뮬레이션에 등장한 모든 수를 마치 첫 번째 수였던 것처럼 통계를 업데이트.
효과: 학습 속도의 비약적 상승. MOGO 등 바둑 프로그램의 핵심 기술.
성능 향상 기법 2: 더 현실적으로 시뮬레이션하기
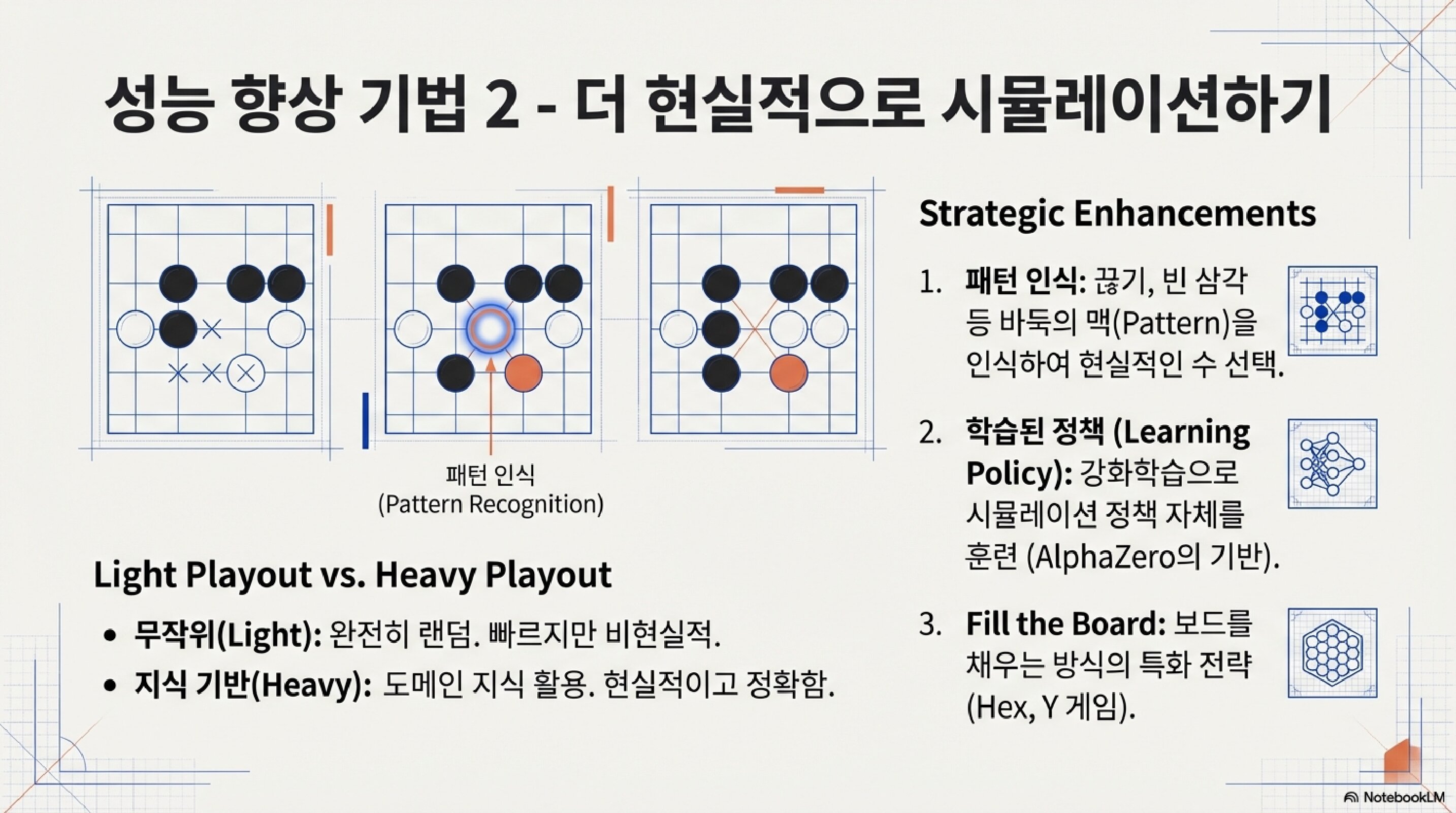
Light Playout vs. Heavy Playout
- 무작위(Light): 완전히 랜덤. 빠르지만 비현실적.
- 지식 기반(Heavy): 도메인 지식 활용. 현실적이고 정확함.
Strategic Enhancements
- 패턴 인식: 끊기, 빈 삼각 등 바둑의 맥(Pattern)을 인식하여 현실적인 수 선택.
- 학습된 정책 (Learning Policy): 강화학습으로 시뮬레이션 정책 자체를 훈련 (AlphaZero의 기반).
- Fill the Board: 보드를 채우는 방식의 특화 전략 (Hex, Y 게임).
게임을 넘어: 조합 최적화
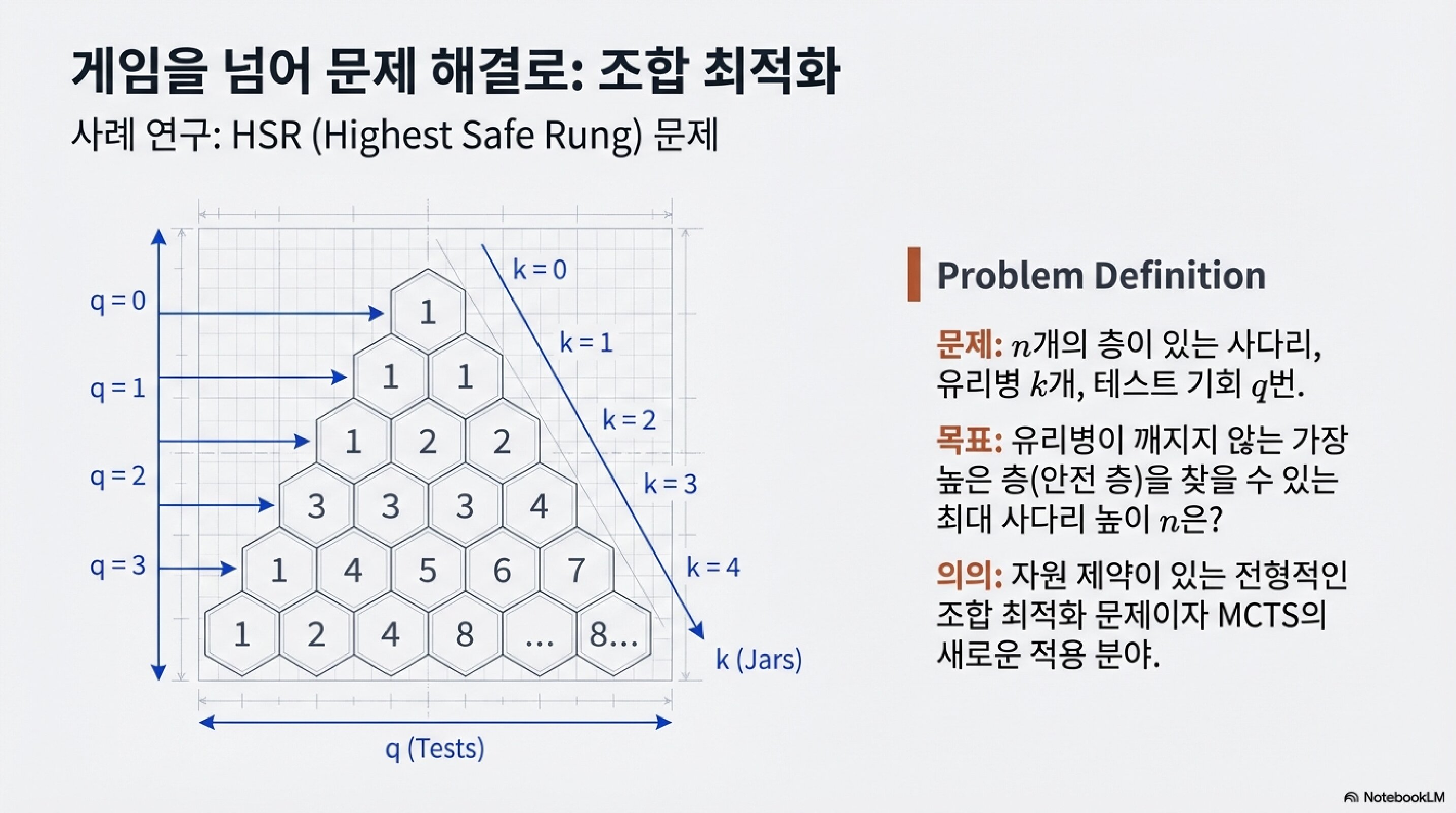
MCTS는 게임만을 위한 게 아니다.
HSR (Highest Safe Rung) 문제
문제: n개의 층이 있는 사다리, 유리병 k개, 테스트 기회 q번.
목표: 유리병이 깨지지 않는 가장 높은 층(안전 층)을 찾을 수 있는 최대 사다리 높이 n은?
의의: 자원 제약이 있는 전형적인 조합 최적화 문제이자 MCTS의 새로운 적용 분야.
Zermelo Gamification
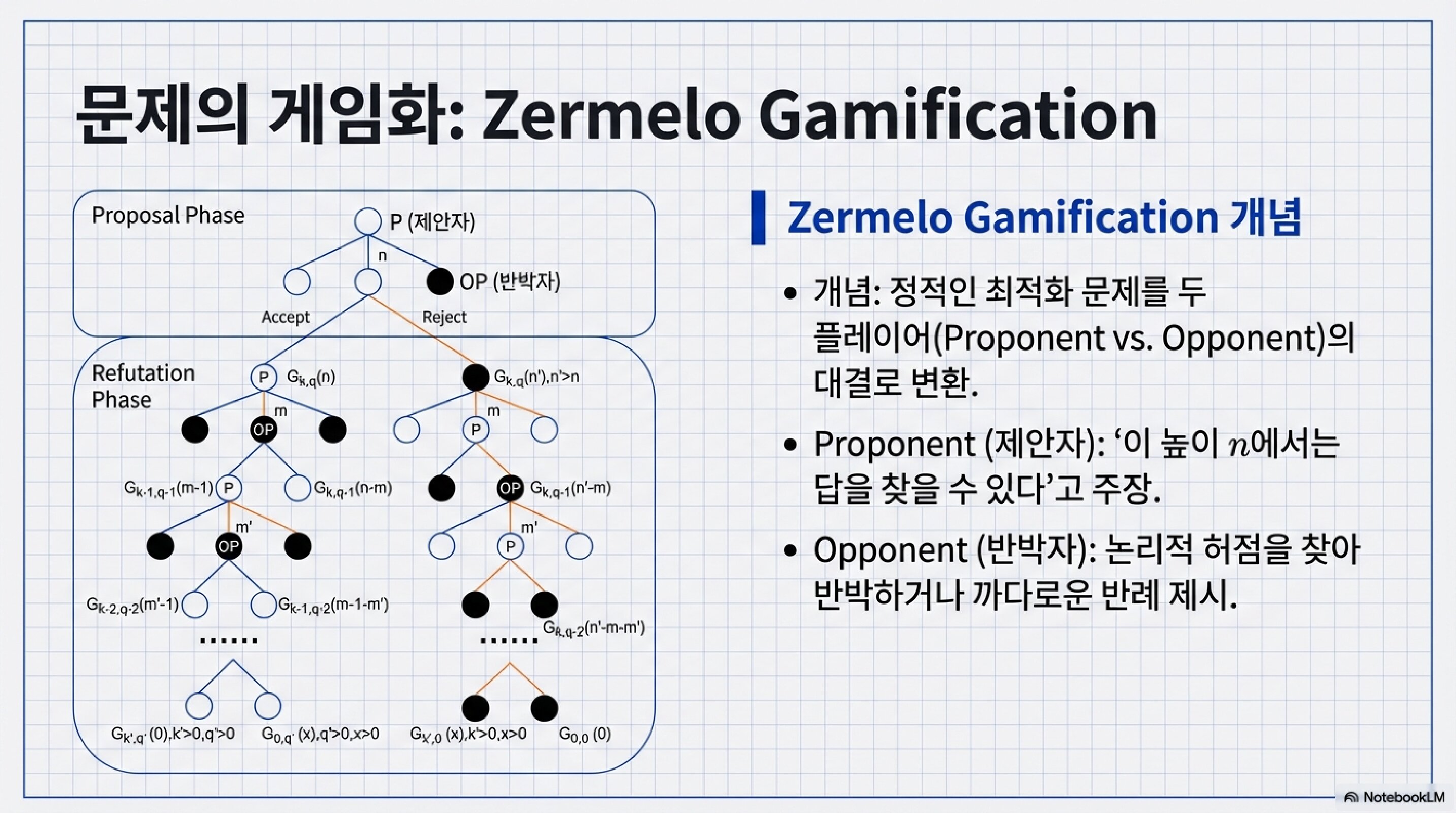
정적인 최적화 문제를 두 플레이어의 대결로 변환.
- Proponent (제안자): “이 높이 n에서는 답을 찾을 수 있다”고 주장
- Opponent (반박자): 논리적 허점을 찾아 반박하거나 까다로운 반례 제시
이렇게 하면 MCTS를 그대로 적용할 수 있다!
Neural MCTS: AlphaZero의 탄생
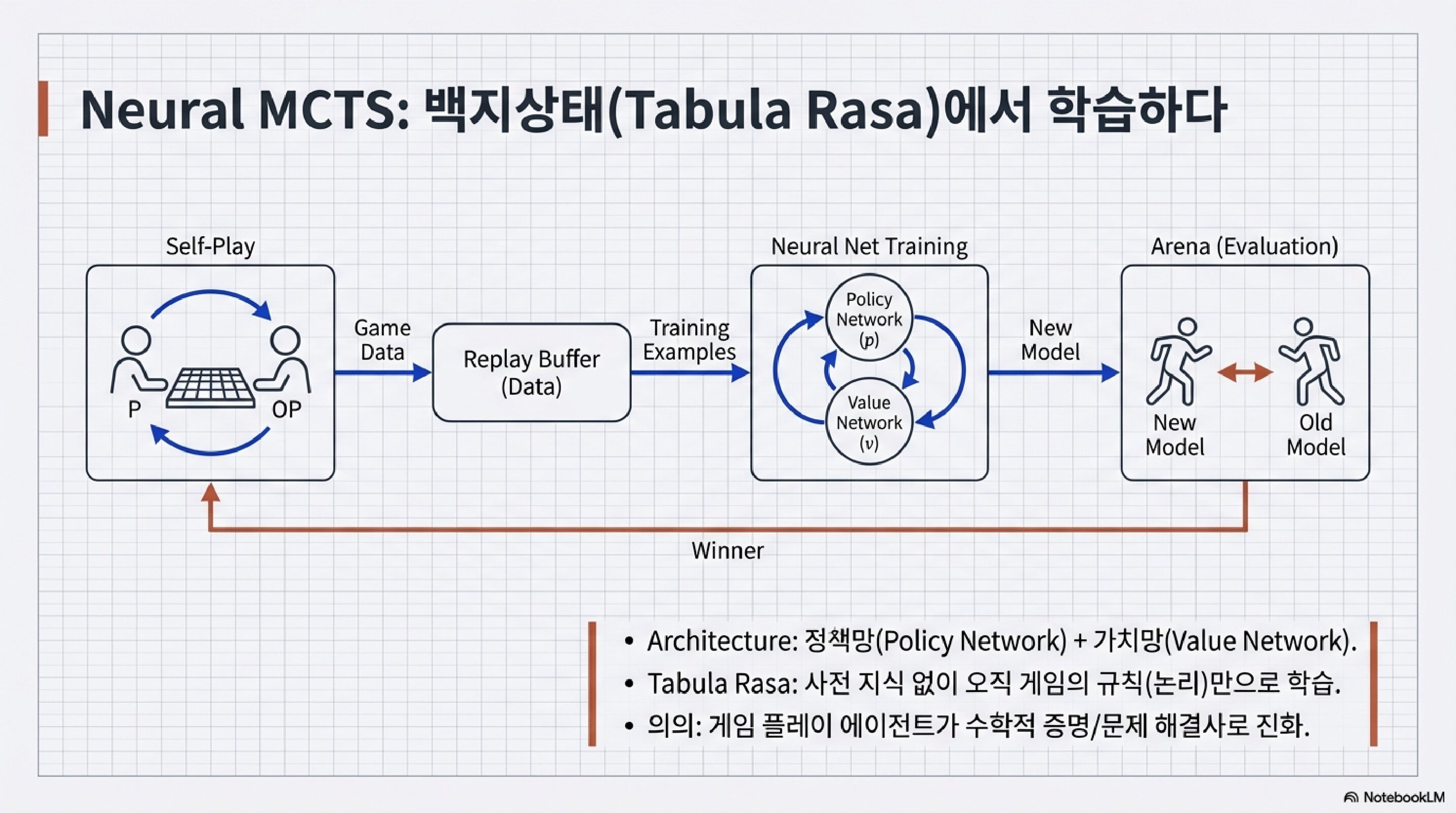
여기서 혁명이 일어났다.
기존 MCTS
- 시뮬레이션: 무작위 플레이아웃
- 느리고, 정확도 낮음
AlphaZero의 Neural MCTS
- 시뮬레이션을 신경망이 대체
- Policy Network: “어디에 둘까”
- Value Network: “누가 이기고 있나”
Tabula Rasa (백지상태)
사전 지식 없이 오직 게임의 규칙(논리)만으로 학습.
게임 플레이 에이전트가 수학적 증명/문제 해결사로 진화.
실험 결과: 스스로 최적해를 찾아내다
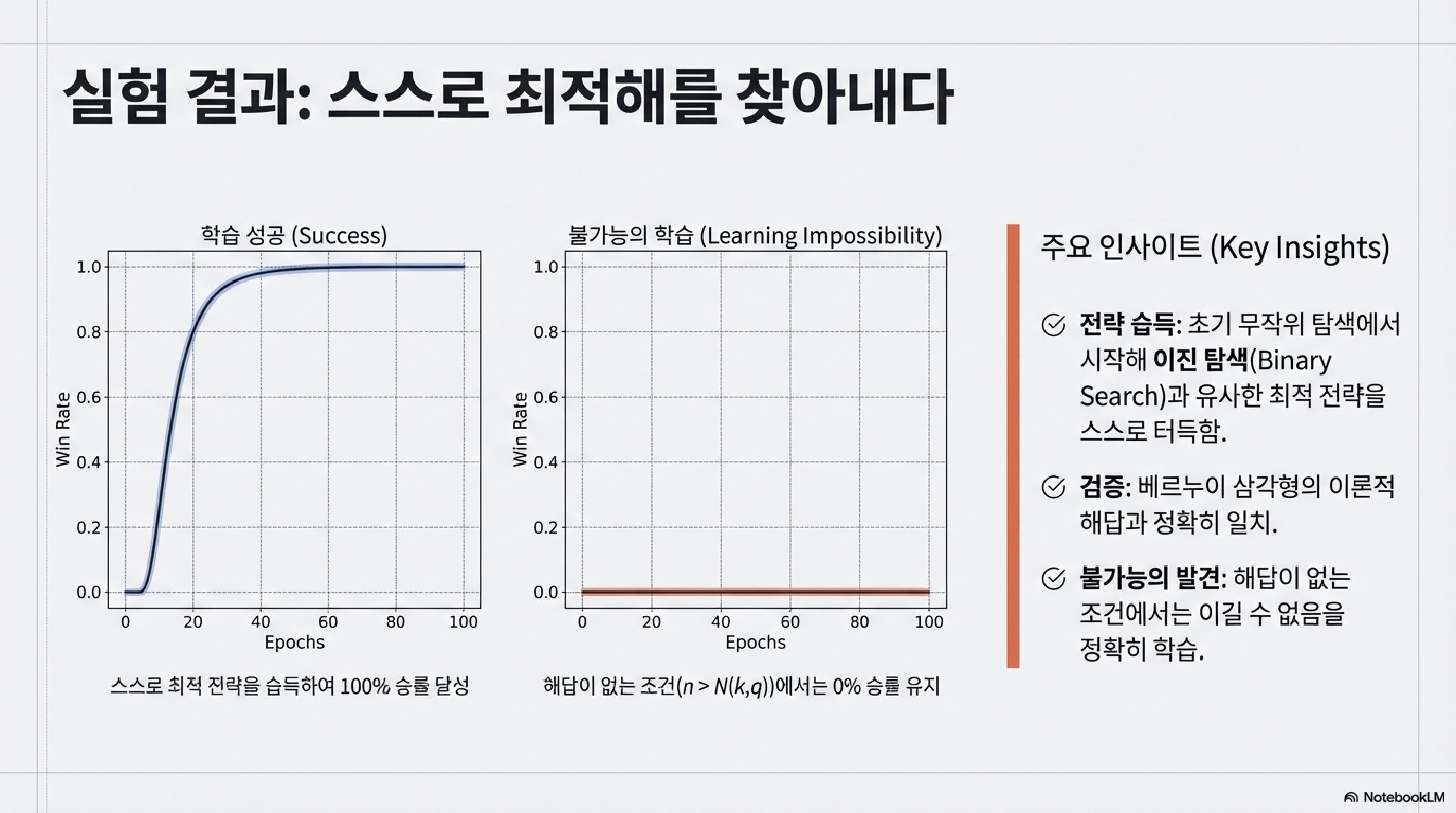
학습 성공 (Success)
스스로 최적 전략을 습득하여 100% 승률 달성.
무작위 탐색에서 시작해 이진 탐색(Binary Search)과 유사한 최적 전략을 스스로 터득.
검증
베르누이 삼각형의 이론적 해답과 정확히 일치.
불가능의 발견
해답이 없는 조건(n > N(k,q))에서는 이길 수 없음을 정확히 학습.
0% 승률 유지.
MCTS의 강점과 한계

강점 (Strengths)
Aheuristic: 도메인별 평가 함수가 없어도 동작 가능.
Anytime: 언제 중단해도 그 시점의 최적해 반환.
Asymmetric: 유망한 경로에 자원을 집중하는 효율성.
한계 (Limitations)
Trap States: 함정 상태(몇 수 뒤 필패)가 많은 도메인에서는 Minimax보다 취약할 수 있음.
Parameter Sensitivity: 탐험 상수(c) 등 파라미터 튜닝이 성능에 결정적 영향.
결론: 직관과 논리의 결합, 그리고 AGI

MCTS는 단순한 탐색 알고리즘이 아니다.
강화학습(RL)과 결합하여 인간의 직관(Neural)과 컴퓨터의 논리(Tree Search)를 통합하는 프레임워크다.
Future Outlook
- 과학적 발견
- 물류 최적화
- 수학적 증명
불확실성 속에서의 복잡한 문제 해결을 위한 핵심 엔진.
핵심 메시지
무작위성(Randomness)을 통해 확실성(Certainty)을 구축하다.
우리 바둑 AI도 이 원리를 사용한다.
매 수마다 수백 번의 시뮬레이션을 돌리고,
그 통계를 바탕으로 최선의 수를 선택한다.
처음엔 무작위로 시작하지만,
반복할수록 진실에 수렴한다.
이게 MCTS의 철학이다.
그리고 어쩌면, 배움의 본질이기도 하다.
다음 편: “밤새 학습한 AI — 셀프플레이 50회 후 일어난 일”
핵심 개념 정리
| 개념 | 설명 |
|---|---|
| UCT | 탐험과 활용의 균형을 맞추는 수식 |
| Playout | 게임 끝까지 시뮬레이션 |
| AMAF/RAVE | 학습 속도 향상 기법 |
| Neural MCTS | 신경망 + MCTS (AlphaZero) |
| Zermelo Gamification | 최적화 문제를 게임으로 변환 |
참고 문헌
- Browne et al. – MCTS Survey
- Kocsis & Szepesvári (2006) – UCT 알고리즘
- Silver et al. – AlphaGo / AlphaZero
